Partial Wave Analysis
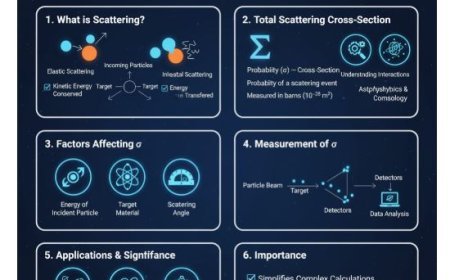
Partial Wave Analysis (PWA) is a fundamental method in quantum mechanics and particle physics used to study scattering phenomena. It breaks down complex interactions, such as particle collisions or wave scattering, into simpler components known as partial waves, each representing a specific angular momentum state. By decomposing the scattering process into these components, scientists can better interpret experimental data, identify fundamental forces, and predict physical outcomes. PWA is widely applied in high-energy physics, nuclear physics, and molecular physics to analyze scattering amplitudes, cross-sections, and interaction dynamics.

Partial Wave Analysis
- An important theory in physics is called Partial Wave Analysis (PWA). It is used to study how particles and quantum mechanics spread light.
- It is a powerful tool that breaks down complicated exchanges into smaller, easier-to-handle parts.
Analysis of Partial Waves
- A scientific method called Partial Wave Analysis is used to examine particle scattering.
- When particles collide, they can scatter off each other, changing their direction and energy.
- The idea behind PWA is to use smaller wave functions to describe this scattering process, each corresponding to a specific angular momentum state of the system.
Important Ideas
1. Waves and Angular Momentum
- Wave functions describe particles in quantum physics.
- Angular momentum is a measure of a particle’s rotational motion. Each wave can carry angular momentum.
- A partial wave is a wave broken into components with different angular momentum values.
2. Scattering
- Scattering is the interaction between particles that alters their motion after a collision.
- The process of scattering creates different wave states, which can be analyzed separately.
Why Partial Wave Analysis is Important
PWA plays a crucial role in various areas of physics, including:
- Simplifying Complex Interactions: Breaking down complicated scattering processes into simpler wave components allows for better understanding.
- Data Interpretation: PWA helps scientists analyze particle collision data, offering insights into fundamental forces and particles.
- Predictive Capability: It enables physicists to predict collision outcomes, which can then be tested in experiments.
How Does Partial Wave Analysis Work?
PWA follows a systematic approach to studying scattering phenomena:
1. Setting Up the Problem
- Incident Waves: Define the incoming particles or waves that interact within the system.
- Interaction Region: Identify the area where scattering occurs, which depends on factors like particle energy and type.
2. Decomposing Waves
- Legendre Polynomials: Express the outgoing waves using Legendre polynomials, which describe rotational motion.
- Partial Wave Amplitudes: Construct partial wave amplitudes, where each amplitude represents a wave with specific angular momentum.
3. Analyzing the Amplitudes
- Determine the contribution of each partial wave amplitude.
- Apply conservation laws (energy and momentum) to formulate equations describing scattering behavior.
4. Fitting Actual Data
- Compare experimental data with PWA predictions.
- Adjust parameters and coefficients of the partial waves to match the observed results.
5. Extracting Physical Data
- Use fitted amplitudes to determine physical quantities, such as cross-sections, which measure the probability of scattering events.
Applications of Partial Wave Analysis
PWA has been widely applied in multiple fields of physics, including:
- High-Energy Physics: Helps analyze particle collisions at CERN and other laboratories, studying interactions between quarks, gluons, and fundamental particles.
- Nuclear Physics: Examines how nucleons scatter within atomic nuclei, providing insights into nuclear forces and structures.
- Molecular Physics: Used to study atomic and molecular interactions, aiding in the understanding of chemical reactions.
What's Your Reaction?