Operator Formalism
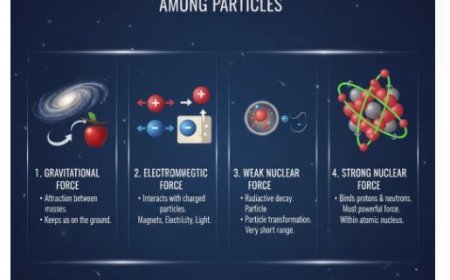
The Operator Formalism is a fundamental framework in physics and quantum mechanics that uses mathematical operators to describe measurable quantities and system transformations. Operators act as linear maps on vector spaces, preserving their structure and allowing for elegant representation of physical laws. Key types include Hermitian operators (for real eigenvalues representing observable quantities), Unitary operators (which preserve inner products and describe quantum evolution), and Projection operators (used to map vectors onto subspaces). Operator formalism plays a vital role in quantum theory, electromagnetism, and statistical mechanics, where operators like the Hamiltonian govern system dynamics and energy behavior.

Operator Formalism
- In physics, an operator is a mathematical tool that transforms one vector space into another.
- Operator theory is essential in various fields of physics, including quantum mechanics, electromagnetism, and statistical mechanics.
Fundamental Ideas
Operators
- Operators are linear maps that act on vector spaces. They can be represented as matrices or functions that operate on vectors.
- Linear operators preserve the linearity of a vector space, meaning that for any two vectors v and w, and any scalar c, the following property holds:
This equation states that applying the operator L to the sum of cvcvcv (where ccc is a constant) and www results in the sum of c times L(v) and L(w).
Different Kinds of Operators
Unitary Operators
- Unitary operators preserve the inner product of vectors, meaning they describe transformations that do not change the norm (length) of vectors.
- Mathematically, a unitary operator U satisfies:
where U† is the Hermitian adjoint (conjugate transpose) of UUU, and III is the identity
operator.
Hermitian Operators
- Hermitian operators, also known as self-adjoint operators, satisfy the condition:
H=H∗
where H∗ (or H†) represents the conjugate transpose of H.
- These operators are important in quantum mechanics because their eigenvalues are always real, which is necessary for representing measurable physical quantities like energy and momentum.
Projection Operators
- Projection operators map vectors onto a subspace of the vector space. They satisfy the property:
P2=P
-
- The eigenvalues of a projection operator are either 0 or 1, meaning they either eliminate a component of a vector or preserve it entirely.
Uses of Operator Formalism
Quantum Mechanics
- In quantum physics, operators represent observable physical quantities such as position, momentum, and energy.
- The eigenvectors of these operators correspond to the possible outcomes of measurements, while the eigenvalues give the actual measured values.
- The Hamiltonian operator
represents the total energy of a system and governs its time evolution through Schrödinger’s equation:
Electromagnetism
- In electromagnetism, operators describe how electric and magnetic fields interact.
- Differential operators, such as the gradient (∇), divergence∇⋅), and curl (∇×), are used in Maxwell’s equations to describe the behavior of electromagnetic fields.
Statistical Mechanics
- In statistical mechanics, operators help describe the equilibrium properties of physical systems.
- The density matrix operator is used to describe the statistical state of quantum systems, forming the basis of quantum statistical physics.
What's Your Reaction?