The Wave (Eigen) Function

The Wave (Eigen) Function

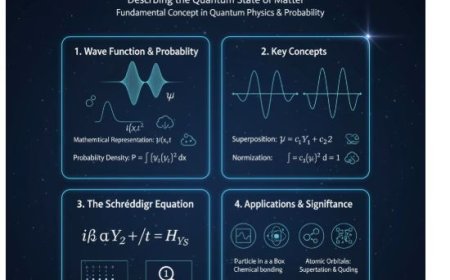
• The wave function, often represented by the Greek letter  (Ψ), is a fundamental concept in quantum physics. It describes the state of a quantum system and provides information about the probability of finding a particle in a specific location and state.

1. Wave Function

• A wave function is a mathematical representation of the quantum state of an object.
• It contains information about the probability of a particle’s position, velocity, and other physical properties.

Mathematical Representation

The wave function is typically represented as Ψ(x,t) where:

• X denotes position,
• t represents time,
• Ψ(x,t) gives a complex-valued probability amplitude.

2. The Role of the Wave Function in Quantum Mechanics

Probability Amplitude

• The wave function determines the probability of finding a particle in a particular state.
• The square of its absolute value gives the probability density.
• To find the probability PPP of locating a particle within a certain region, we integrate the probability density over that area:

Superposition Principle

• Quantum systems can exist in multiple states simultaneously. The wave function represents this concept using superposition, meaning different states can combine to form a new wave function.
• Mathematically, if Ψ1​ and Ψ2 are two wave functions, then:

where  c1​ and c2 are coefficients that determine the contribution of each state.

3. Solving the Wave Equation

Schrödinger Equation

• The evolution of a wave function is governed by the Schrödinger equation, which is fundamental in quantum mechanics.
• The time-dependent form of the equation is:

where:

• (h-bar) is the reduced Planck’s constant,
• H is the Hamiltonian operator, which represents the total energy of the system.

Eigenstates and Eigenvalues

• Solutions to the Schrödinger equation are called eigenstates. Each eigenstate corresponds to a specific eigenvalue, which usually represents observable quantities like energy.
• When a measurement is performed on a quantum system, the wave function collapses to one of its eigenstates, and the observed value corresponds to the associated eigenvalue.

4. Understanding the Wave Function Physically

Normalization

• The wave function must be normalized so that the total probability of finding the particle anywhere in space is equal to one:

• The wave function is generally complex, meaning it has both real and imaginary parts. This complexity leads to interference effects, which are fundamental in quantum mechanics.

5. Uses of Wave Functions

Quantum Mechanics

• Wave functions are applied in various areas of quantum mechanics, including:
• Particle in a box,
• Quantum harmonic oscillators,
• Atomic orbitals (describing electron distributions in atoms).

Quantum Chemistry

• In quantum chemistry, wave functions describe how electrons behave and interact in atoms and molecules. This understanding is crucial for explaining chemical bonding and reactions.

Quantum Computing

• Wave functions are essential in quantum computing, as qubits can exist in superposition states, representing different quantum possibilities simultaneously.