Particle in a Box

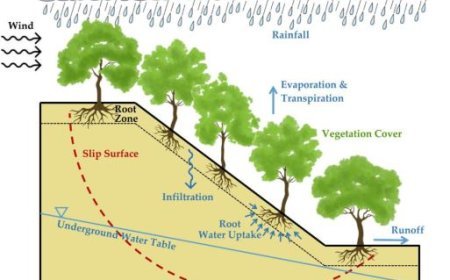
The Particle in a Box model is a cornerstone of quantum mechanics, describing how a particle, such as an electron, behaves when confined within a rigid, impenetrable region. Represented as an infinite potential well, the model shows that a particle can only occupy discrete energy levels, leading to the concept of quantization. This simple yet powerful model helps explain the wave function, probability distribution, and zero-point energy of quantum systems. It also provides a foundation for understanding real-world phenomena like quantum dots, molecular orbitals, and electron transitions in atoms.

ARUL PRASANTH ARUL PRASANTH
May 17, 2022 - 02:15 Updated: Jun 14, 2026 - 23:47
0 61
Particle in a Box

Particle in a Box

  • The "Particle in a Box" model is one of the most important concepts in quantum physics.
  • It demonstrates the fundamental behavior of quantum particles in a simplified system.

 

1. Introduction to Quantum Mechanics

Quantum Mechanics

  • Quantum mechanics is the branch of physics that studies how particles behave at the atomic and subatomic levels.
  • Classical physics describes a deterministic universe, but quantum mechanics introduces uncertainty and probability into our understanding of nature.

 

Particle in a Box

  • The "Particle in a Box" model simplifies quantum physics by providing an idealized system.
  • This model considers a particle, such as an electron, trapped inside a small, rigid region (the "box").
  • It helps explain fundamental quantum principles without requiring complex mathematics.

 

2. Concept of the Box

Infinite Potential Well

  • The box is modeled as an infinite potential well, meaning:
    • Inside the box: The potential energy is zero.
    • Outside the box: The potential energy is infinite, preventing the particle from escaping.

 

Dimensions of the Box

  • The box is often considered one-dimensional for simplicity.
  • However, the model can also be extended to two or three dimensions.

 

Boundaries of the Box

  • Walls of the Box: The walls are impenetrable, meaning the particle bounces back whenever it reaches a wall.
  • Length of the Box: The energy levels and wave functions of the particle depend on the width of the box (L).

 

3. Wave Functions and Quantum States

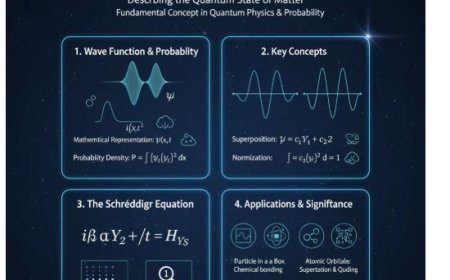
Wave Function (Ψ)

  • The wave function (Ψ) is a mathematical function that describes the probability of finding a particle in a particular state or location.
  • Inside the box, the wave function behaves like a standing wave that fits within the given boundaries.

 

Allowed Wave Functions

The wave function must satisfy the following conditions:

  1. Boundary Condition
    • At the edges of the box, x = 0 and x = L, the wave function must be zero:
      Ψ(0) = 0 and Ψ(L) = 0.
  2. Normalization Condition
    • The total probability of finding the particle inside the box must be 1, meaning:
      ∫ |Ψ(x)|² dx = 1 over the range 0 to L.

 

4. Quantization of Energy Levels

  • A particle in a box has discrete energy levels, meaning it cannot have just any energy value.
  • The energy levels are given by the formula:

Eₙ = (n²h²) / (8mL²)

where:

    • Eₙ = Energy at level n
    • n = Positive integer (quantum number)
    • h = Planck’s constant
    • m = Mass of the particle
    • L = Length of the box

 

5. Implications of the Model

Probability Distribution

  • The probability density of finding the particle at a certain location is given by |Ψ(x)|².
  • Depending on the energy level, the particle is more likely to be found in certain regions of the box.

Zero-Point Energy

  • According to the Heisenberg Uncertainty Principle, a particle can never be completely at rest.
  • Even in the ground state (n = 1), the particle still has energy, called zero-point energy.

 

6. Real-World Applications

The "Particle in a Box" model helps explain many physical phenomena, including:

Quantum Dots

  • Quantum dots are tiny semiconductor structures that trap electrons in three dimensions.
  • Their energy levels behave like those in a particle-in-a-box system.

Molecular Orbitals

  • The way electrons occupy energy levels in atoms and molecules is similar to a particle in a box.
  • Electrons in chemical bonds exist at discrete energy levels.

 

Understanding Quantum Systems

  • This model provides a foundation for studying more complex quantum systems.
  • It helps explain phenomena like quantum tunneling, electron transitions, and the quantum behavior of gases.

Explore Subject Categories

• StudySpot360 Home: https://studyspot360.com/

• Geology Study Materials: https://studyspot360.com/geology

• Physics Notes and Learning Resources: https://studyspot360.com/physics

• English Grammar and Study Materials: https://studyspot360.com/english

About StudySpot360

StudySpot360 is a trusted educational platform providing high-quality study materials, detailed notes, MCQs, quizzes, question papers, and academic resources across multiple subjects. Our mission is to make reliable educational content accessible to students, educators, researchers, and lifelong learners while supporting academic excellence, examination preparation, and continuous learning.

Explore more educational articles, tutorials, practice questions, quizzes, and subject-wise learning resources to strengthen your knowledge and continue your learning journey with StudySpot360.

 

Tags: