Representation Theory and Identical Particles in Quantum Mechanics
Representation theory plays a crucial role in quantum mechanics, offering a mathematical framework to describe symmetry, conservation laws, and the behavior of identical particles such as bosons and fermions. By studying how physical systems transform under symmetry operations, representation theory helps organize quantum states and understand particle interactions. The variation method, a key approximation technique, further supports this by estimating a system’s ground state energy using trial wave functions. Together, these concepts deepen our understanding of quantum symmetries, wave function construction, and the statistical behavior of identical particles in physics.
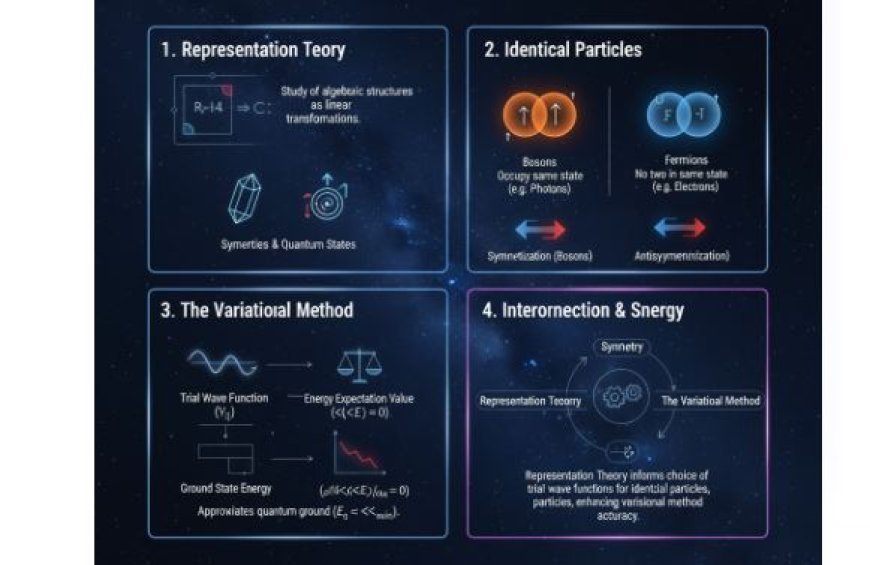
Representation Theory and Particles That Are Identical
- In quantum physics, it is very important to understand how particles behave.
- The point of this piece is to look into the physics ideas of representation theory, similar particles, and the variation method and show how these ideas are linked.
1. An Introduction to the Theory of Representation
1.1 The Theory of Representation
- In mathematics, representation theory is the study of abstract algebraic structures by showing their parts as linear changes of vector spaces.
- Representation theory is a part of physics that helps us understand symmetries and conservation rules, especially in quantum mechanics.
1.2 Why It's Important in Physics
- Symmetries: A lot of physical systems have symmetries, and representation theory lets scientists use math to explain these features.
- Quantum States: It helps us organize quantum states based on their symmetry qualities, which makes it easier to study systems of particles that are all the same.
2. Quantum Mechanics: Particles That Are the Same
2.1 What It Means
- In quantum mechanics, identical particles are particles that can't be told apart from each other.
- Examples include electrons, protons, and rays.
2.2 Types of Particles That Are the Same
- Bosons:
- Particles that follow the rules of Bose-Einstein statistics.
- They can be in the same quantum state as other bosons.
- Example: Photons.
- Fermions:
- Particles that follow the Pauli exclusion principle and Fermi-Dirac statistics.
- No two fermions (like electrons) can be in the same quantum state at the same time.
2.3 Stabilization and Loss of Stabilization
- Bosonic Particles:
- Use symmetrization, meaning the wave function remains the same when any two particles are switched.
- Fermionic Particles:
- Use antisymmetrization, meaning swapping two particles changes the sign of the wave function.
3. The Variation Method in Quantum Mechanics
3.1 The Variation Method is What It Sounds Like
- The variation method is a way to get close to a quantum system's ground state energy.
- It is based on trial wave functions and quantum physics principles.
3.2 Steps to Follow for the Variation Method
- Pick Out a Trial Wave Function:
- Pick a function that is close to the system's real wave function.
- This method often has options that can be changed.
- Figure Out the Expectation Value:
- Use the trial wave function to figure out the expectation value of the energy.
- This gives a rough estimate of how much energy the system has.
- Minimization:
- Change the trial wave function's settings to lower the predicted energy.
- The lowest value of the expected energy tells us how much the true ground state energy is.
- Evaluate the Results:
- Use known answers or other methods to check the accuracy of the estimate.
3.3 Use Cases
- Complex Systems: The variation method works best for systems where it's hard to find a perfect answer.
- Quantum Chemistry: Used to figure out the structure and characteristics of molecules.
4. How Representation Theory, Identical Particles, and the Variation Method Are Related
4.1 What Symmetry Does
- Symmetry considerations are important in understanding systems of identical particles.
- Representation theory helps choose the correct trial wave functions in the variation method.
4.2 Building Wave Functions
- Knowing representation theory is essential for building wave functions for identical bosonic or fermionic objects.
- This knowledge can help improve the variation method by guiding the selection of trial functions.
What's Your Reaction?