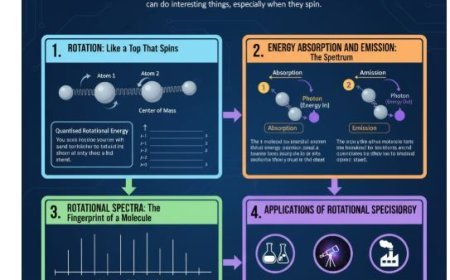
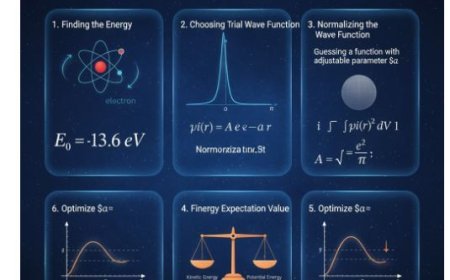
Linear Harmonic Oscillator – Definition, Motion, and Applications

Linear Harmonic Oscillator

• A basic idea in physics is the linear harmonic oscillator, which shows how an object moves as it swings back and forth around a set point known as the equilibrium position.
• Many natural events, like the vibration of a guitar string, the movement of a pendulum, and the motion of a spring-mass system, show this kind of motion.

Definition of a Linear Harmonic Oscillator

• A linear harmonic oscillator is a system made up of a spring and a mass. The spring constant is k.
• The mass is moved out of its equilibrium position and then released, which makes it move back and forth around its equilibrium position.
• This equation describes the motion of the mass:

F = -kx

where:

• F is the force acting on the mass,
• k is the spring constant,
• x is the displacement of the mass from its equilibrium position.

Characteristics of a Linear Harmonic Oscillator

There are a few main features of a linear harmonic oscillator that define its motion:

1. Periodic Motion
• The motion of a linear harmonic oscillator is periodic, meaning it repeats at regular intervals over a fixed time period (T).
2. Simple Harmonic Motion (SHM)
• The motion of a linear harmonic oscillator follows simple harmonic motion (SHM).
• SHM is a type of periodic motion where the acceleration of the object is proportional to its displacement from the equilibrium position.
3. Constant Amplitude
• The amplitude (A) remains constant over time.
• This means that the maximum displacement of the mass from its equilibrium position stays the same.
4. Constant Frequency
• The frequency of a linear harmonic oscillator remains constant over time.
• This means that the number of oscillations per second stays the same.

Equations of Motion

The motion of a linear harmonic oscillator can be described using the following equations:

1. Equation of Motion
• The displacement of the mass at any time t is given by:
• x(t) = A cos(ωt + φ)
• where:
• x(t) is the displacement at time t,
• A is the amplitude,
• ω is the angular frequency,
• φ is the phase angle.
2. Velocity Equation
• The velocity of the mass is found by differentiating the displacement equation
• with respect to time:
• v(t) = -Aω sin(ωt + φ)
3. Acceleration Equation
• The acceleration of the mass is found by differentiating the velocity equation with respect to time:
• a(t) = -Aω² cos(ωt + φ)

Energy of a Linear Harmonic Oscillator

• The total energy of a linear harmonic oscillator is conserved, meaning it remains constant over time.
• The total energy (E) of the system is given by:

E = (1/2) k A²

where:

• E is the total energy,
• k is the spring constant,
• A is the amplitude.

Importance of Linear Harmonic Oscillator

The linear harmonic oscillator is one of the most fundamental concepts in physics and has many applications in various fields:

1. Mechanical Systems
• The linear harmonic oscillator helps in understanding the motion of systems like pendulums, vibrating strings, and springs.
2. Electrical Circuits
• It is used in electrical engineering to describe the behavior of LC and RLC circuits.
3. Quantum Mechanics
• The linear harmonic oscillator is used to model quantum systems, such as the quantum harmonic oscillator potential.