The Klein-Gordon Equation in Relativistic Quantum Mechanics

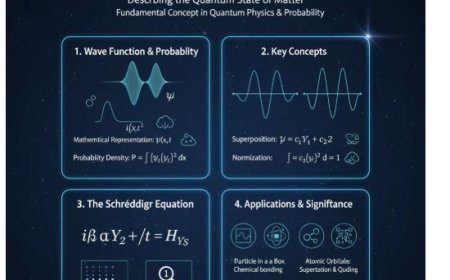
The Klein-Gordon Equation

The Klein-Gordon equation is a fundamental equation in theoretical physics that defines scalar particles (particles with no intrinsic structure or spin, such as the Higgs boson) within the context of relativistic quantum mechanics.

1. Origin and Motivation

• Relativistic Quantum Mechanics: The Schrödinger equation, which regulates particle motion in quantum mechanics, does not include special relativity. The Klein-Gordon equation was created to address this difficulty and describe particles that travel at almost the speed of light.
• Relativity and Wave Nature: The equation includes two main principles:
• Relativity refers to particle travel at relativistic speeds, which are close to light speed.
• Quantum Mechanics: The concept that particles exhibit wave-like properties.

2. The Klein-Gordon Equation

The Klein-Gordon equation may be expressed as:

Where:

• The scalar field ϕ\phiϕ represents a particle's wave function.
• The second time derivative ∂2∂t2\frac{\partial^2}{\partial t^2}∂t2∂2​ explains how the wave function varies over time.
• The Laplacian operator ∇2\nabla^2∇2 defines the wave function's dispersion in space.
• The particle's mass is denoted by mmm.
• The equation is in natural units, with c=1c = 1c=1 (representing the speed of light).

3. The Components of the Equation

• The term ∂2∂t2\frac{\partial^2}{\partial t^2}∂t2∂2​ refers to the change in the wave function with time, comparable to how a particle's location changes in classical mechanics.
• The spatial operator ∇2\nabla^2∇2 represents the dispersion of the wave function in space, similar to particle diffusion.
• The particle's mass m2m^2m2 affects the wave function's behavior throughout time and space.

4. Key Concepts for the Klein-Gordon Equation

A. Wave Function ϕ(x,t)\phi(x,t)ϕ(x,t)

• In quantum physics, the wave function describes a particle's state.
• The function ϕ(x,t)\phi(x,t)ϕ(x,t) defines the chance of discovering a scalar particle at a specific point and time.

B. Relativistic Energy-Momentum Relation

The Klein-Gordon equation is based on the relativistic energy-momentum connection:

Where:

• EEE represents the particle's total energy.
• ppp represents momentum.
• mmm is the particle's mass.
• The symbol ccc represents the speed of light.

The Klein-Gordon equation may be expressed using:

5. Interpreting the Klein-Gordon Equation

• The equation describes the behavior of a particle's wave function over time and space. It ensures that particles follow both quantum mechanics and relativity.
• The Klein-Gordon equation, unlike the Schrödinger equation, permits particles to move at relativistic speeds. This is crucial for high-energy physics, including particle accelerators and cosmology.

6. Solutions for the Klein-Gordon Equation

• The Klein-Gordon equation may be expressed as a plane wave solution, similar to classical waves, representing a free particle:

Where:

• AAA represents the amplitude.
• The wave vector kkk is connected to momentum.
• Frequency ω\omegaω is connected to energy.

These solutions are significant because they represent particle motion through space-time.

7. Applications for the Klein-Gordon Equation

• Quantum Field Theory (QFT): The Klein-Gordon equation describes scalar fields, such as the Higgs field. Particles are considered as excitations of fields.
• Particle Physics: It is used in studying high-energy particles and quantum fields, including the Higgs boson and other fundamental particles.
• Cosmology: The equation aids in understanding the early universe, where particles may move at relativistic speeds.