The Harmonic Oscillator in Matrix Theory
The harmonic oscillator in matrix theory provides a mathematical framework for modeling oscillatory systems using matrices. Represented by a 2×2 matrix, the harmonic oscillator describes periodic motion governed by a restoring force proportional to displacement. The eigenvalues of the system matrix determine the angular frequency (ω), while the eigenvectors define the oscillation’s magnitude and phase. This approach is essential in quantum mechanics, classical mechanics, and engineering, where oscillations, damping, and resonance are key phenomena. Matrix representation also allows precise modeling of damped and forced oscillators in complex systems.
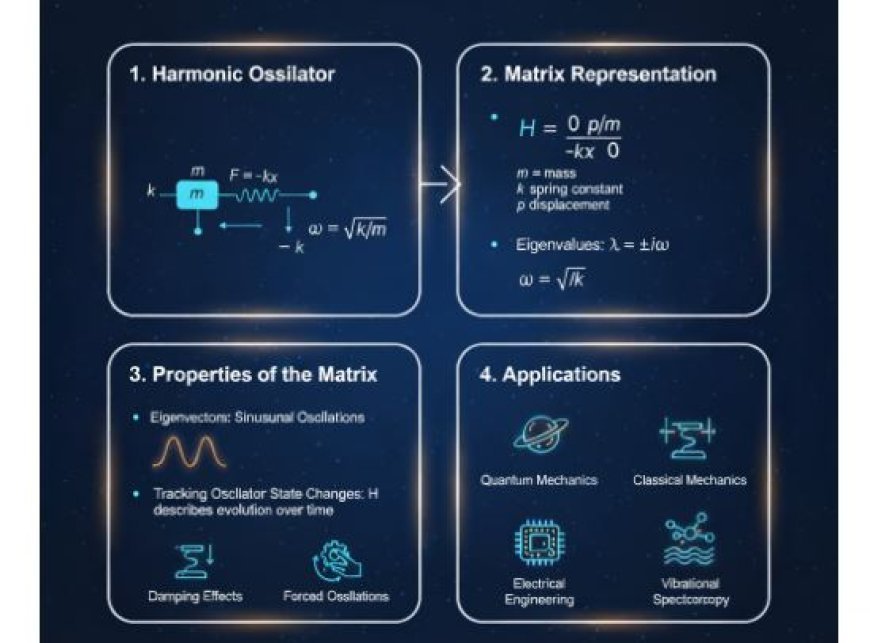
The Harmonic Oscillator in Matrix Theory
- Matrix theory is a branch of physics that uses mathematical matrices to model physical systems.
- One of its fundamental applications is modeling harmonic oscillators, which are systems that oscillate periodically.
Harmonic Oscillator
- A harmonic oscillator is a system that oscillates periodically around its equilibrium point.
- The restoring force acting on the oscillator is proportional to its displacement from equilibrium, leading to sinusoidal oscillations.
Matrix Representation of a Harmonic Oscillator
In matrix theory, a harmonic oscillator can be represented using the following 2×22 \times 22×2 matrix:
- mmm is the mass of the oscillator.
- kkk is the spring constant.
Properties of the Matrix
The angular frequency ω\omegaω of the oscillator is determined by the eigenvalues of the matrix HHH:
The eigenvectors of HHH describe the magnitude and phase of the oscillations.
Applications of Harmonic Oscillators in Matrix Theory
Harmonic oscillators modeled using matrices have applications in various fields:
- Quantum Mechanics: Models particle motion in potential energy wells.
- Classical Mechanics: Describes oscillatory behavior in systems such as springs and pendulums.
- Electrical Engineering: Analyzes oscillating circuits and resonant systems.
- Vibrational Spectroscopy: Studies molecular vibrational modes.
Other Properties and Features
- Eigenvalues and Eigenvectors: The eigenvalues and eigenvectors of HHH form complex conjugate pairs, confirming that the oscillations are sinusoidal.
- Tracking Oscillator State Changes: The matrix HHH can be used to describe how the oscillator evolves over time.
- Damping Effects: A damping term can be added to the matrix equation to account for frictional forces.
- Forced Oscillations: Modifying the matrix elements allows for the inclusion of external forces, leading to forced oscillations.
What's Your Reaction?