FLUID DYNAMICS

FLUIDS DYNAMICS

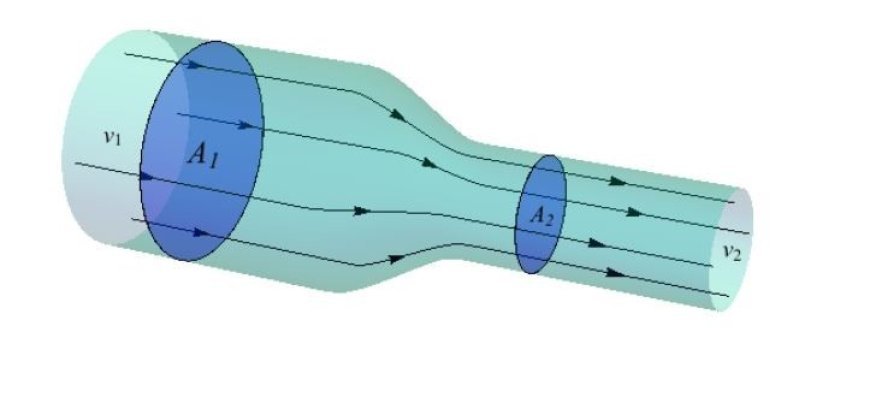
• The rate at which mass leaves a system is equal to the rate at which mass enters a system. This is known as the continuity equation in fluid dynamics.
• This is how the differential form of the continuity equation looks:

The most important part of the continuity equation is how it is written in math:
∂ρ/∂t + ∇ ∙ (ρu) = 0

Let's break it down

• ∂ρ/∂t: This term shows how fast the density (ρ) changes over time (t). This change is zero in a steady-state flow, which means the density stays the same throughout the system.
• ∇ ∙ (ρu): This is the net rate at which mass moves into or out of a small volume element in the system. It is also called the divergence of the mass flux.
• The divergence (∇) operator figures out how much the flow "concentrates" or "spreads out" around a certain point.

1. u: This is the flow velocity vector field. It shows the fluid's direction and speed at all points in the system. So, the equation basically says that the net flow of mass into or out of a volume (∇ ∙ (ρu)) must equal the rate of change of density within that volume (∂ρ/∂t). In simple words, in a steady-state flow, what goes in minus what goes out must equal zero.

Applications of the Continuity Equation

This equation, which seems easy, has a lot of uses in many areas:
Aerodynamics: Aerodynamics is the study of how the air moves around aeroplane wings to figure out their lift and drag forces.

Hydraulics: making sure that the input and output masses are adjusted when designing pipe systems for water or oil flow.

Astrophysics: studying how gas clouds move between stars and how stars and galaxies are formed.

Combustion Engines: Testing how fuel and air move inside engines to get the best performance and fuel economy.

Beyond the Equation

• It's only the tip of the iceberg when it comes to fluid mechanics. Once you understand it, you can look into other interesting ideas, such as
• Bernoulli's equation shows how pressure, speed, and height are related to fluid flow.
• Navier-Stokes equations: they describe how viscous flows move while taking friction and internal forces into account.
• Computational fluid dynamics (CFD) is the study of complicated fluid flows using computer simulators.

IMAGE SOURCE (THUMBNAIL)