Born-Oppenheimer Approximation

Born-Oppenheimer Approximation

• An important idea in quantum mechanics, especially in molecular physics and chemistry, is the Born-Oppenheimer estimate.
• When you separate the movements of nuclei and electrons, it makes molecular processes easier to understand.
• The ideas behind the Born-Oppenheimer approximation will be broken down in a clear and simple way in this piece. 

1. Introduction to the Born-Oppenheimer Approximation

• What it means: In quantum chemistry, the Born-Oppenheimer approximation is a way to make the complicated interactions between systems with many particles, like molecules, easier to understand by assuming that the motions of nuclei and electrons can be handled independently.
• History: This idea was first put forward by scientists Max Born and Robert Oppenheimer in the early 1900s, which helped modern quantum chemistry grow.

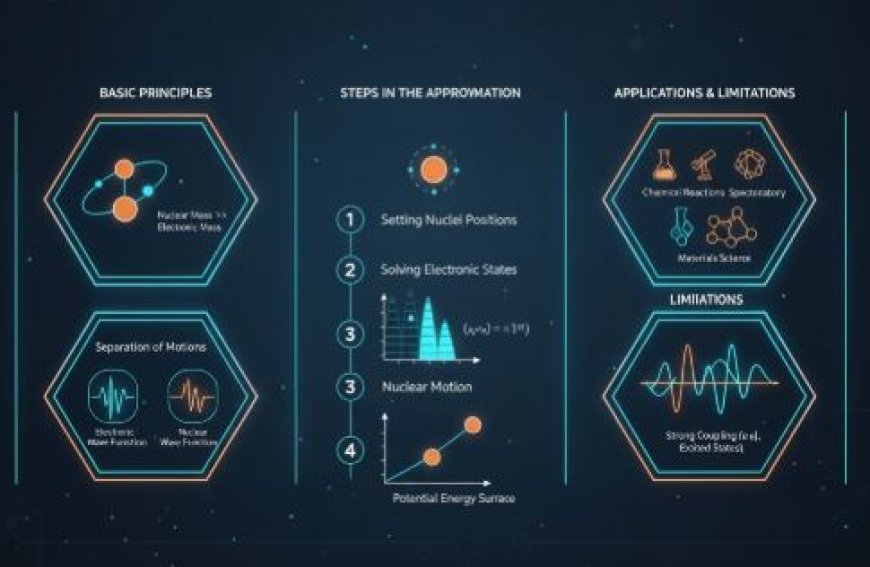
2. Basic Principles

• Nuclear Mass vs. Electronic Mass:
• Nuclei are much heavier than electrons in molecules.
• Because of this big difference in mass, nuclei move much more slowly than electrons.
• Separation of Motions:
• The approximation takes into account this difference in mass, which lets scientists separate the motion of nuclei and electrons.
• The total wave function of a molecular system can be written as the result of:
• An electronic wave function that is based on electronic coordinates.
• A nuclear wave function that is based on nuclear coordinates.

3. Steps in the Born-Oppenheimer Approximation

Step 1: Setting the Positions of the Nuclei

• The positions of the nuclei are kept fixed when figuring out how the electrons in a molecule behave.
• This makes it possible to simplify the Schrödinger equation and only look at the electrons.

Step 2: Solving for Electronic States

• If you set the nuclei, you can solve the electronic wave functions.
• These wave functions give you the electronic energies as a function of where the nuclei are fixed.

Step 3: Nuclear Motion

• The nuclei can move after the electric states have been found.
• The energies from the electronic solutions are used to make potential energy surfaces for the atoms.
• This lets you figure out how the nucleus is moving using either classical or quantum physics.

4. The Born-Oppenheimer Approximation Has Some Benefits

• Makes calculations easier:
• Complex many-body problems can be solved by separating the movements of nuclei and electrons.
• Use in Molecular Dynamics:
• Potential energy surfaces obtained from electronic states can be used to study nuclear motion.
• This makes it easier for researchers to study how molecular systems change over time.

5. Limitations

• Here's a breakdown of close interactions:
• The approximation might not work when the movements of electrons and nuclei are strongly connected.
• This happens in cases such as excited states changes or when nuclei are very light.
• Not Good Enough for Some Systems:
• The estimate can be wrong for some molecules, especially those where the nuclei and electrons are strongly coupled in vibrational or rotational ways.

6. Applications

• Understanding transition states and reaction paths in chemical reactions is an important part of learning about reactions.
• Spectroscopy: Reading energy levels and changes in molecular spectra to learn more about them.
• Material science: The study of the qualities of complicated materials and the creation of new compounds.