A Semi-Classical Look at the Zeeman Effect
The Zeeman Effect describes the splitting of atomic energy levels when an atom is placed in an external magnetic field, resulting from the interaction between the atom’s magnetic dipole moment and the field. First observed by Pieter Zeeman in 1896, this phenomenon causes spectral lines to divide into multiple components, revealing key insights into atomic and magnetic properties. The semi-classical approach combines classical motion (electron orbits and spins) with quantum mechanics, using concepts like angular momentum, Landé g-factor, and Bohr magneton to describe how magnetic fields alter atomic energy. The effect is classified into Normal Zeeman Effect (triplet splitting) and Anomalous Zeeman Effect (complex splitting due to spin-orbit coupling). The Zeeman Effect finds applications in spectroscopy, astrophysics, and magnetic field measurements, offering a powerful tool for studying atomic structure and cosmic magnetism.
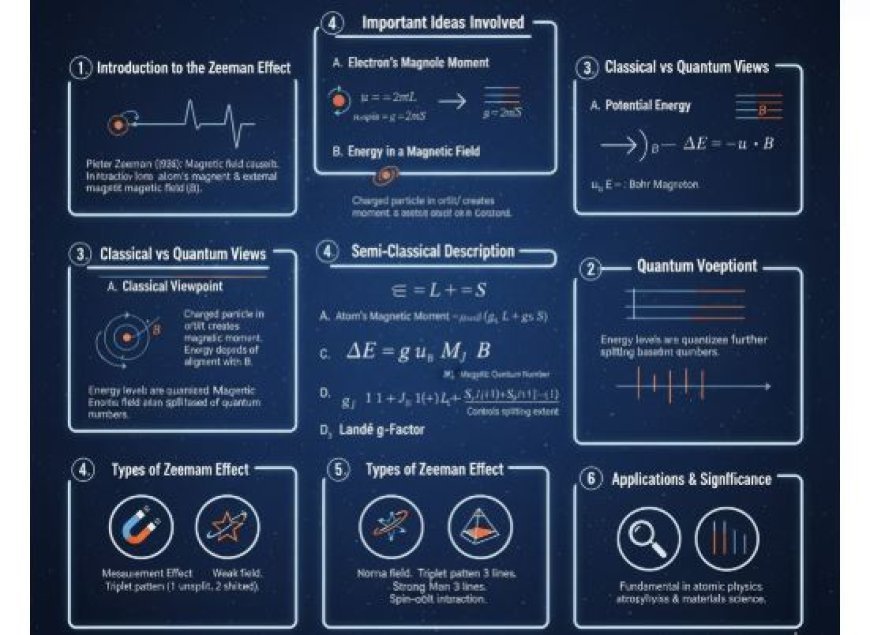
A Semi-Classical Look at the Zeeman Effect
When there is a magnetic field around, the Zeeman effect occurs, which causes the energy levels of atoms to split. This happens due to the interaction between the magnetic field and the atom's magnetic dipole moment. As a result, the energy levels break into multiple components.
1. A Brief Look at the Zeeman Effect
- The Zeeman effect was first observed by Pieter Zeeman in 1896. When an atom is placed in a magnetic field, its spectral lines split. This is due to the interaction between the atom's magnetic moment (which arises from its orbital and spin angular momentum) and the external magnetic field.
- This effect is commonly observed in atomic spectra, particularly in the presence of strong magnetic fields.
2. Important Ideas Involved
A. An Electron's Magnetic Dipole Moment
- An electron moving around an atom creates a magnetic moment, which is proportional to its orbital angular momentum.
- The magnetic moment of an electron due to its orbital motion is given by:
where:
- μ = Magnetic moment
- e = Charge of the electron
- m = Mass of the electron
- L = Orbital angular momentum
- The spin of the electron also contributes to the total magnetic moment. The spin magnetic moment is given by:
where:
- μ_spin = Magnetic moment due to spin
- S = Spin angular momentum
- g = g-factor (a constant related to the electron's spin, approximately 2 for an electron)
B. Energy of an Electron in a Magnetic Field
- When an electron with a magnetic moment is placed in an external magnetic field (B), its potential energy is given by:
- This interaction causes a shift in the atom's energy levels. The magnitude of this shift depends on the alignment of the magnetic moment with the magnetic field.
3. The Roles of Classical and Quantum Mechanics
Both classical and quantum mechanical approaches help explain the Zeeman effect.
A. The Classical Viewpoint
- Classically, an electron can be thought of as a charged particle moving in a circular orbit (creating orbital angular momentum) or spinning on its own axis (creating spin angular momentum). This motion generates a magnetic moment, which interacts with the external magnetic field.
- The splitting of energy levels can be understood as electrons occupying different positions in the magnetic field, each gaining or losing energy differently.
- Quantum mechanics refines this idea, stating that an electron's angular momentum and energy levels are quantized. When exposed to a magnetic field, these quantized energy levels split further according to the quantum numbers.
4. A Semi-Classical Look at the Zeeman Effect
- The total angular momentum (J) of an electron is given by:
where:
-
- J = Total angular momentum
- L = Orbital angular momentum
- S = Spin angular momentum
B. An Atom's Magnetic Moment
- The total magnetic moment of an atom is the sum of contributions from both orbital and spin angular momentum:
where:
-
- μ_total = Total magnetic moment
- g_L = Orbital g-factor (approximately 1)
- g_S = Spin g-factor (approximately 2 for an electron)
C. Energy Splitting in a Magnetic Field
When an atom is placed in a magnetic field, the energy levels split due to the interaction between the total magnetic moment and the field. The energy shift is given by:
where:
- ΔE = Energy shift
- μ_B = Bohr magneton (a physical constant related to the electron's magnetic moment)
- g = Landé g-factor
- J = Total angular momentum quantum number
- M_J = Magnetic quantum number of the total angular momentum
- B = External magnetic field
D. Landé g-Factor
The Landé g-factor determines the degree of energy splitting in atoms with multiple electrons. It is calculated using:
This factor accounts for both orbital and spin contributions to the total angular momentum and controls the extent of energy splitting.
5. Types of Zeeman Effect
The Zeeman effect is classified into two main types based on the strength of the magnetic field:
A. Normal Zeeman Effect
- Occurs when the magnetic field is weak compared to the separation between energy levels.
- The energy levels split into three components:
- One remains unchanged
- Two shift in opposite directions
- This produces a triplet pattern in the spectral lines.
B. Anomalous Zeeman Effect
- Occurs when the magnetic field is strong enough that the spin-orbit interaction significantly affects the splitting.
- The energy levels split into more than three components, leading to a more complex pattern in spectral lines.
- The fine structure of atomic lines makes this effect more prominent.
6. Applications of the Zeeman Effect
The Zeeman effect is widely used in physics, especially in spectroscopy and astrophysics.
- Measurement of Magnetic Fields:
-
- The Zeeman effect is used to determine the strength of magnetic fields in various environments, such as laboratories or astronomical observations.
- Astrophysics:
-
- Helps analyze magnetic fields of stars and planets by observing how light from these celestial objects splits into spectral lines.
- Spectroscopy:
-
- Used to study the fine structure of atomic energy levels and interactions between magnetic fields and atoms.
What's Your Reaction?