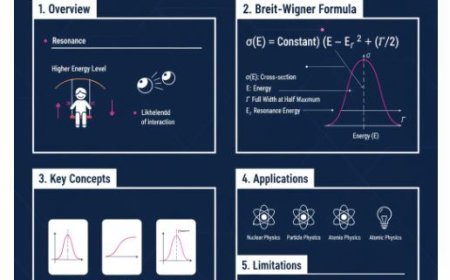
DIFFERENTIATOR AND INTEGRATOR
Differentiators and Integrators: Opposite Ends of the Signal Spectrum
- The words for the electronic devices that do math processes like differentiation and integration are differentiator and integrator, respectively.
- This chapter goes into a lot of detail about differentiators and integrators that use op-amps.
- Please keep in mind that these are also examples of linear op-amp applications.
Differentiator
- A differentiator is a type of mechanical system that gives off an output that is equal to the first derivative of its input.
- This part goes into more depth about the op-amp-based differentiator.
- An op-amp-based differentiator produces an output that is equal to the differential of the input voltage that is applied to its inverting terminal.
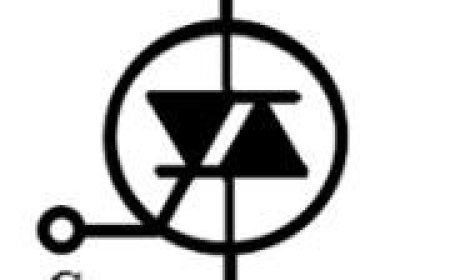
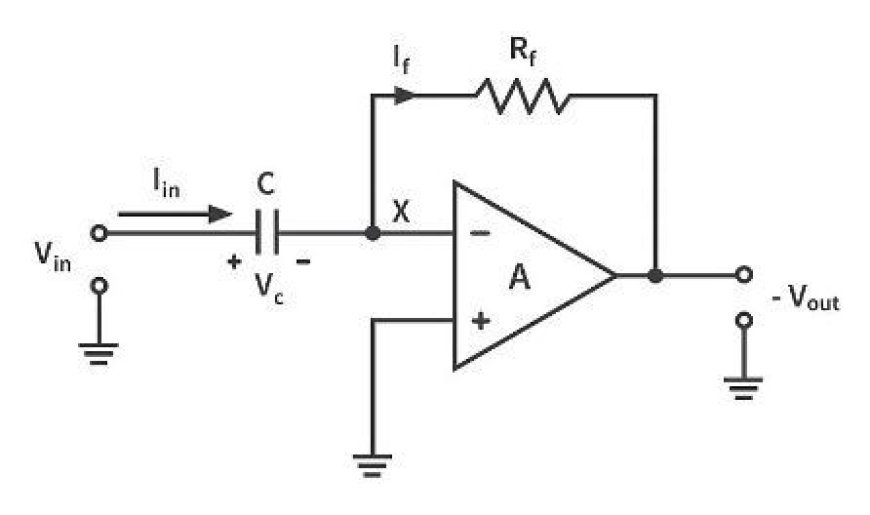
- These pictures show the circuit design of a divider that uses an op-amp:
- In the above circuit, the non-inverting input wire of the op-amp is linked to ground. That means zero voltage is given to its non-inverting input terminal.
- The voltage at the opamp's inverting input terminal will be identical to the voltage at its non-inverting input terminal, according to the virtual short principle.
- In this case, there will be no voltage at the inverting input terminal of the op-amp.
Integrator
- An integrator is an electronic device that makes an output that is the integration of the given input.
- The op-amp-based integrator is talked about in this section.
- An op-amp-based integrator gives off an output that is a sum of the voltages that are applied to its inverting terminal.
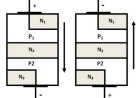
- The following picture shows the circuit diagram of an integrator based on an op-amp:
- Inside the circuit shown above, the op-amp's non-inverting input port is linked to ground. In this case, the non-inverting input line gets no power.
- The voltage at the op-amp's inverting input terminal will be the same as the voltage at its non-inverting input terminal, according to the virtual short idea.
- In this case, there will be no voltage at the inverting input terminal of the op-amp.
What's Your Reaction?
arulprasanth
Arul Prasanth - MSc Geology graduate offering comprehensive study materials in Geology, Physics, and English. With a focus on clarity and effectiveness, I aim to provide students with the tools necessary for academic success.
