Understanding the Breit-Wigner Formula
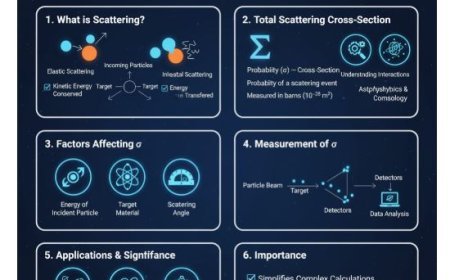
The Breit-Wigner formula explains how resonance affects particle interactions in nuclear and atomic physics. It describes how the reaction cross-section peaks at specific resonance energies, forming a Lorentzian (bell-shaped) curve. Learn how parameters like resonance energy (Eᵣ), full width at half maximum (Γ), and lifetime determine the probability of nuclear or particle interactions. This principle is essential for understanding nuclear reactions, energy levels, and particle discoveries in modern physics.

Breit-Wigner Formula
1. Overview
Resonance happens when a system, such as an atom or particle, is excited to a higher energy level for a brief period. This charged state is unstable and quickly returns to a lower energy state. Think of a swingset: when you push it at just the right times, it goes higher. In physics, resonance increases the effect of interactions at a certain energy level.
- Cross-section: In particle physics, the cross-section represents how likely it is for specific interactions to occur between particles.
- A larger cross-section means a greater chance of interaction.
2. Breit-Wigner Formula
• Summary
The Breit-Wigner formula is a mathematical tool that predicts how likely it is for a resonance to break apart into specific particles. It suggests that the cross-section of a scattering process (where particles collide and change direction) will show a peak at the resonance energy, with a characteristic bell-curve shape (Lorentzian shape).
• Formula:
- σ(E): Cross-section at energy E.
- Γ: Full Width at Half Maximum (FWHM) of the resonance peak. This shows the energy range where the resonance has a significant effect on interactions. A larger Γ means the excited state lasts for a shorter time.
- E_r: Resonance energy (the highest energy point of resonance).
- Mathematical relation:
This formula shows that the maximum value of the cross-section occurs at the resonance energy (E = E_r) and decreases rapidly as energy moves away from this point.
3. Key Concepts
- Lorentzian Shape: The typical bell-shaped curve seen in the resonance peak of the cross-section. It is a defining feature of the Breit-Wigner formula.
- Full Width at Half Maximum (FWHM):
- The width of the resonance peak at half of its maximum value.
- It is inversely related to how long the excited state lasts.
- A shorter-lived state has a wider peak (larger Γ).
- Resonance Energy (E_r):
- The energy level where the resonance peak occurs.
- This is the most probable energy for an interaction.
4. Applications
The Breit-Wigner formula is widely used in different fields of physics, including:
- Nuclear Physics:
- Studying nuclear reactions and the structure of atomic nuclei.
- Determining energy levels within a nucleus.
- Applications in nuclear power plants and nuclear weapons.
- Particle Physics:
- Identifying new particles and analyzing their properties.
- Understanding how fundamental particles, such as quarks and leptons, interact.
- Atomic Physics:
- Explaining energy transitions that occur within atoms.
5. Limitations
- The Breit-Wigner formula is a simplified model and may not fully describe all resonance events.
- In cases where the resonance is very broad or when multiple resonances overlap, more complex formulas are required for better accuracy.
What's Your Reaction?