Adiabatic Approximation

Adiabatic Approximation

• The adiabatic assumption is a very important idea in many areas of physics, especially in quantum mechanics and thermodynamics.
• It makes complicated systems easier to understand by letting us guess how they will act in certain situations.

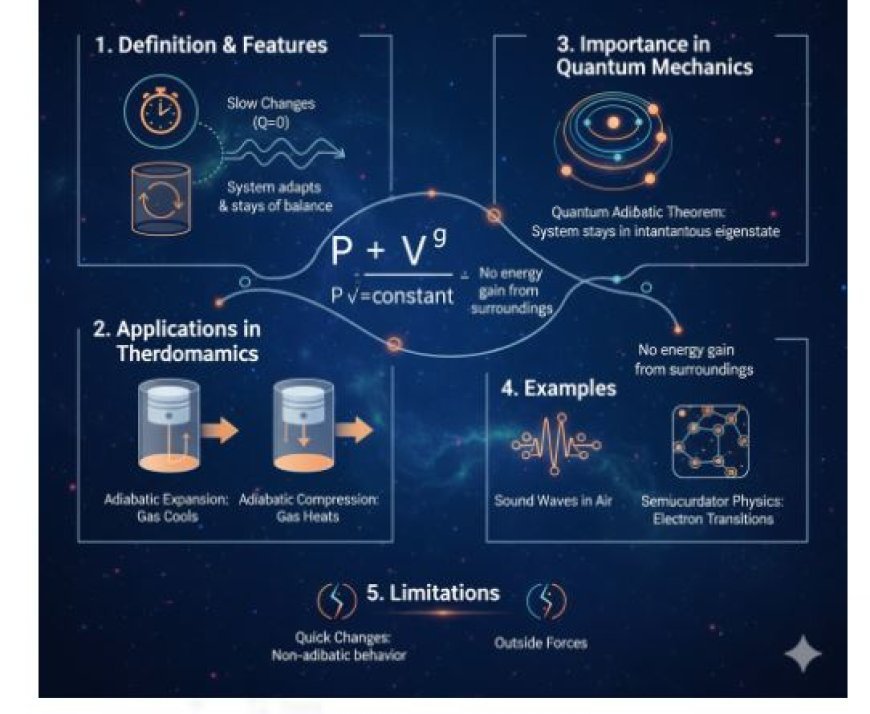
1. Adiabatic Approximation

Definition

• When the features of a system change more slowly than the timescale of its own dynamics, this is called the adiabatic assumption.
• In these situations, the system stays in thermal balance with itself, meaning that it doesn't lose or gain much heat with its surroundings.

Most Important Features

• Slow Changes: The system's factors, such as pressure, volume, or magnetic fields, change slowly enough that the system can adapt and stay in balance.
• No Heat Transfer: The important thing about an adiabatic process is that no heat comes into or goes out of the system. This keeps the system's internal energy constant even when it changes slowly.

2. Applications in Thermodynamics

Adiabatic Processes

In thermodynamics, adiabatic processes are very important for knowing how gases do work.

• Adiabatic Expansion:
• When a gas expands without sharing heat, like in a well-insulated container, it cools down because work is being done.
• Adiabatic Compression:
• On the other hand, adiabatically compressing a gas makes it hotter because the work done on it gives it more energy.

Important Equations

• Most of the time, the adiabatic condition is shown by the equation:

Where:

• P is the pressure.
• V is the volume.
• γ (gamma) is the adiabatic index, which is the ratio of specific heats.

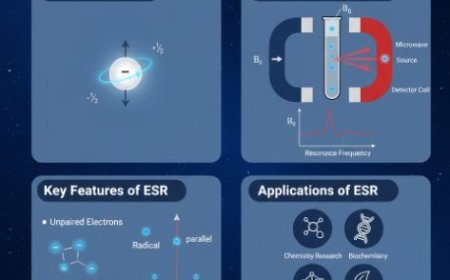
3. Why It's Important in Quantum Mechanics

Quantum Adiabatic Theorem

• You can get to the quantum adiabatic theorem from the adiabatic assumption in quantum physics.
• This theorem says that if slow changes happen to a quantum system, it will move between its quantum states without getting more energy from its surroundings.

How the Theorem Is Used

• Energy Levels: The system stays in its instantaneous eigenstate even though its Hamiltonian changes over time.
• This is a key concept for understanding how molecules move and respond in chemical reactions.

4. Examples of the Adiabatic Approximation

1. Sound Waves in the Air

• As pressure waves, sound waves move through the air.
• The movement in a compression wave is slow enough that the air molecules can keep up with it.
• This means that the sound transfer is essentially adiabatic.

2. Semiconductor Physics

• When it comes to electron transitions in semiconductors, the adiabatic approach helps scientists model how electrons move when electric fields change.
• This happens without giving up energy to the lattice.

5. Limitations of the Adiabatic Approximation

Breakdown Conditions

The adiabatic approach makes calculations a lot easier, but it has some problems:

• Quick Changes:
• If the conditions change too quickly, the system can't keep up, which causes non-adiabatic behavior (when heat exchange becomes important).
• Interactions with Outside Forces or Events:
• The idea of a separate system can also be shown to be false when outside forces or events happen.

Testing Adiabaticity

• Physicists often use experiments or computer simulations to see if a process can be treated adiabatically.
• They make sure that the timescales of changes are long enough.