Bracket Notation

Bracket Notation

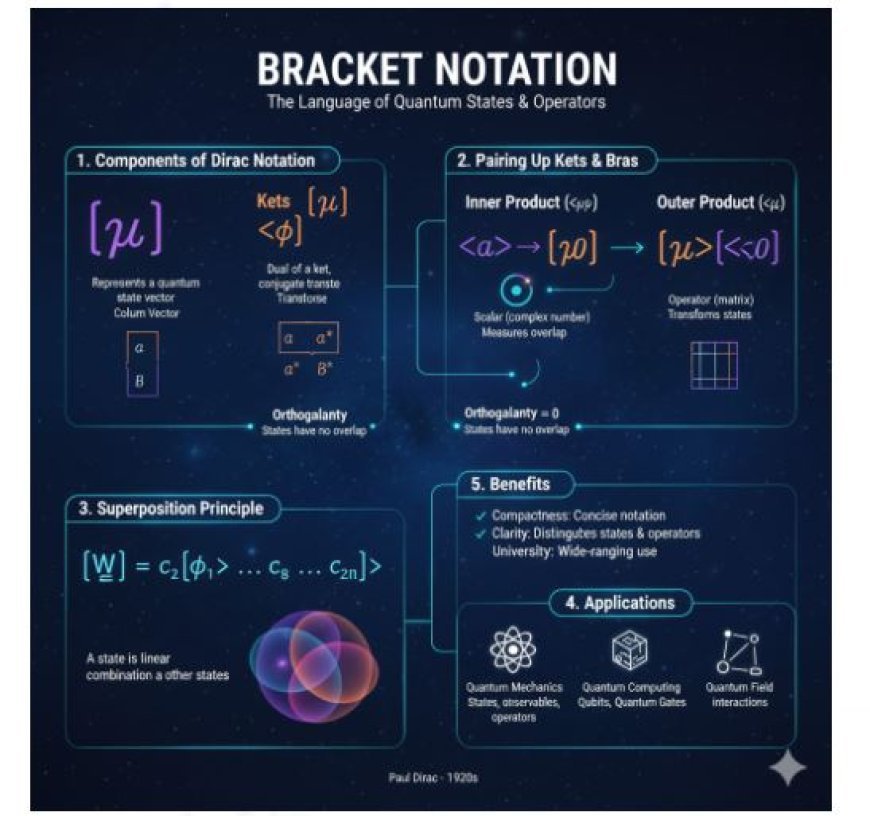
• Bracket notation is a very important tool in physics, especially in areas like linear algebra and quantum mechanics.

Bracket Notation Overview

• Bracket notation, also known as Dirac notation, is a way to describe quantum states and work with them mathematically.
• The physicist Paul Dirac introduced this notation, which is widely used in quantum mechanics.

Components of Bracket Notation

There are two main parts of bracket notation:

1. Kets (∣ψ⟩)

• Represent quantum states.
• The ket symbol ∣⟩ indicates the state of a system in a vector-like form.

2. Bras (⟨ϕ∣)

• Represent the dual or conjugate transpose of kets.
• The bra symbol ⟨∣ is used in operations like inner products.

Pairing Up Kets and Bras

Many operations in quantum physics involve the combination of bras and kets:

• Inner Product (⟨ϕ∣ψ⟩):
• This is the scalar product of two states, which measures how much two quantum states overlap.
• Outer Product (∣ψ⟩⟨ϕ∣):
• Represents an operator that transforms one state into another.

Why Use Bracket Notation?

Bracket notation simplifies complex ideas in quantum physics and offers several benefits:

• Compactness: Compared to standard vector notation, it is more concise.
• Clarity: Clearly distinguishes between operations (inner/outer products), dual states (bras), and states (kets).
• Universality: Used beyond quantum theory, in fields like quantum computing and field theory.

Important Concepts in Bracket Notation

1. Quantum States

• In quantum mechanics, quantum states—represented by kets—are fundamental units.
• Example: A ket like ∣ψ⟩ could describe the state of a particle in a specific configuration.

2. Inner Products

• The inner product (⟨ϕ∣ψ⟩) quantifies the similarity between two quantum states.
• If the inner product is zero, the states are orthogonal, meaning they have no physical overlap.

3. Outer Products

• The outer product (∣ψ⟩⟨ϕ∣) forms an operator, which can be applied to other states.
• This is crucial for discussing quantum measurements and transformations.

4. The Principle of Superposition

• In quantum mechanics, a state can be a linear combination of other states.
• Bracket notation makes it easy to express superpositions:

• Here, c₁, c₂, …, cₙ are coefficients representing the contribution of each basis state to the total state.

Applications of Bracket Notation

1. Quantum Mechanics

• In quantum mechanics, states, observables, and operators are commonly expressed using bracket notation.
• It simplifies writing equations and understanding concepts like superposition and entanglement.

2. Quantum Computing

• Bracket notation plays a key role in quantum computing, where qubits can exist in multiple states simultaneously.
• Quantum gates, which perform operations on qubits, are often represented using bras and kets.

3. Quantum Field Theory

• In advanced physics, bracket notation helps describe particle interactions and field dynamics.
• It makes complex quantum processes more manageable.