De Broglie Wavelength
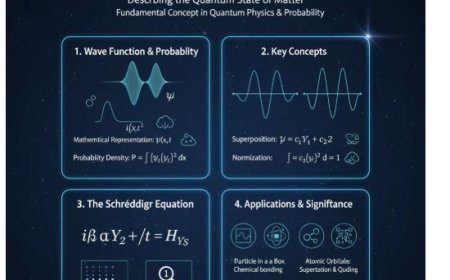
The De Broglie wavelength is a fundamental concept in quantum mechanics that connects wave and particle behavior. Proposed by Louis de Broglie, it shows that every moving particle, like an electron, has a wavelength given by λ = h/p, where h is Planck’s constant and p is the particle’s momentum. This idea explains wave-particle duality and helps describe interference and diffraction patterns of matter at the atomic level.

De Broglie Wavelength
- Wave-particle duality in quantum physics shows that particles like electrons can act like waves.
- A key addition to this idea was made by French physicist Louis de Broglie, who introduced the idea of the "de Broglie wavelength."
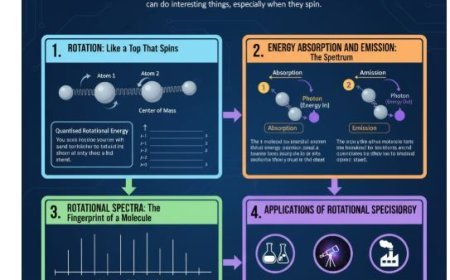
1. Wave-Particle Duality
- Definition: Wave-particle duality is a key idea in quantum physics. It means that every particle can act like both a wave and a particle.
- Significance: Understanding the de Broglie wavelength is important for understanding quantum mechanics, especially how electrons behave in atoms.
2. Wavelength
- Wavelength (λ): The space between two high points of a wave. In classical wave physics, it relates to light waves or other types of electromagnetic waves.
- Relationship between Energy and Wavelength: For light waves, energy and wavelength are directly related. This can be shown with the equation:
In this formula:
- E stands for energy,
- H represents Planck's constant,
- c is the speed of light,
- λ is the wavelength.
Introducing the de Broglie Hypothesis
- De Broglie's Proposition: Louis de Broglie suggested that if light can act like both a wave and a particle, then objects such as electrons should also show wave-like behaviour.
- De Broglie Wavelength: He described the wavelength of a moving particle using this formula:
Where:
- λ is the de Broglie wavelength,
- h is Planck's constant,
- p is the momentum of the particle.
3. How to Find the De Broglie Wavelength
Step 1: Learn About Momentum
- Momentum (p): In classical physics, momentum is given by:
where:
-
- m is the particle's mass,
- v is its speed.
Step 2: Connecting to Energy
- Kinetic Energy (K.E.): The kinetic energy of the particle can be written as:
- Using Energy Relationship: We can link kinetic energy and motion through the connection between energy and wavelength for light.
Step 3: Apply Einstein’s Relation
- Energy-Mass Relation:
Einstein’s well-known equation,
explains how energy and mass are related when things move very fast. However, for our reasoning, we focus on:
- This can also be adapted for massive particles in the non-relativistic case by the de Broglie theory.
Step 4: Merging the Relationships
By setting our earlier equations equal to each other, we see that the momentum of a particle can be used in the wave equation:
4. Importance of the De Broglie Wavelength
- Wave-Particle Behaviour: The formula explains that all matter, like electrons and protons, has a wavelength. This means that particles can show interference patterns, just like light waves do.
- Applications: The de Broglie wavelength is important in areas like quantum physics, thermodynamics, and studying atoms and smaller particles.
What's Your Reaction?