Derivation of Schrödinger’s Equation
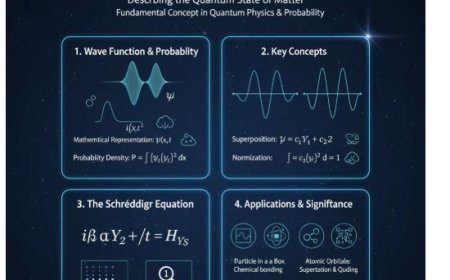
The Schrödinger equation is the foundation of quantum mechanics, describing how the quantum state of a system evolves over time. Derived from the concepts of wave-particle duality, quantized energy, and the classical wave equation, it mathematically explains how particles behave as waves. The time-dependent and time-independent forms of Schrödinger’s equation help predict energy levels, wave functions, and particle behavior at the atomic level.
Derivation of Schrödinger's Equation
Schrödinger's Equation in Quantum Physics
- Schrödinger's equation is one of the most important ideas in quantum physics. It shows how a quantum system changes over time.
I. Introduction
- Newton's rules, which show how an object's position, speed, and acceleration are related, describe how a particle moves in classical mechanics.
- When we get to the quantum world, though, the rules of traditional physics no longer hold true. Wave-particle duality is introduced by quantum physics.
- Particles can behave in both wave-like and particle-like ways. Schrödinger's equation gives us a new way to think about maths that lets us explain this behaviour.
II. Two Types of Particles and Waves
- Albert Einstein came up with the special theory of relativity in 1905. It went against the long-held belief that time and space are fixed.
- Later, in 1924, Louis de Broglie came up with the idea of wave-particle duality, which says that particles like electrons can behave like waves.
- Experiments, like the famous double-slit experiment, helped to prove this idea even more.
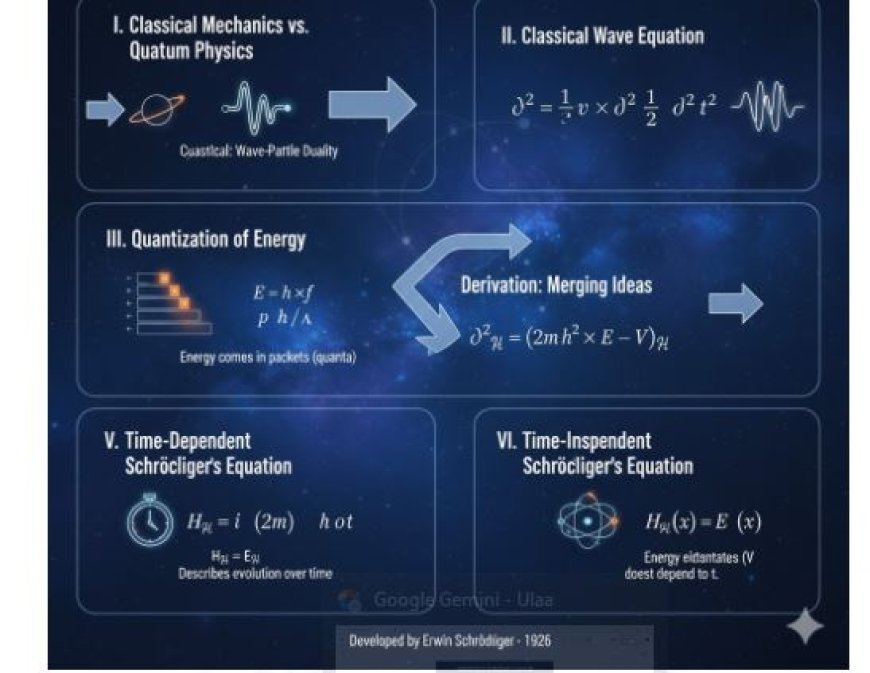
III. Classical Wave Equation
- We need to start with the classical wave equation in order to understand how Schrödinger's equation came to be.
- The classical wave equation shows how waves, like sound waves or light waves, move through a substance.
- It is written as:
∇²ψ = (1 / v²) × (∂²ψ / ∂t²)
- Where:
- ψ is the wave function
- v is the wave's speed
- ∇² is the Laplacian operator
IV. Quantization of Energy
- Quantum physics says that energy is quantized, which means that it comes in discrete packets (quanta) instead of being a constant stream.
- In classical physics, energy is thought to be continuous, so this is a big change.
- An equation that shows how energy is quantized is given below:
E = h × f
- Where:
- E is energy
- h is Planck's constant
- f is the frequency of the wave
V. Derivation of Schrödinger's Equation
- We need to put together the classical wave equation and the idea of quantized energy to get Schrödinger's equation.
- First, let's say that the wave function (ψ) depends on both time (t) and position (x).
- After that, we put the energy formula (E = h × f) into the classical wave equation:
(1 / v²) × ∇²ψ = ∂ψ / ∂t
- A new form of the energy equation that uses the de Broglie relation (p = h / λ) is:
E = p² / 2m
- This formula fits into the classical wave equation, giving us:
∇²ψ = (1 / v²) × (∂²ψ / ∂t²) = (2m / h²) × (E – V)ψ
-
- Where:
- V is the potential energy
- Where:
VI. Time-Dependent Schrödinger Equation
- Introducing the idea of time dependence is the last step.
- There is a chance that the wave function (ψ) changes with both time (t) and place (x).
- The time-dependent Schrödinger equation is given by:
Hψ = iℏ × (∂ψ / ∂t)
- Where:
- i is the imaginary unit
- ℏ is the reduced Planck's constant (h / 2π)
- ψ is the wave function
VII. Time-Independent Schrödinger's Equation
- The potential energy (V) doesn't always change with time, and the wave function (ψ) can be split into:
- A spatial part: ψ(x)
- A time-dependent part: e^(-iEt/ℏ)
- The time-independent Schrödinger equation is given by:
Hψ(x) = Eψ(x)
- The energy eigenstates of the system are shown by this equation.
What's Your Reaction?