The Ehrenfest Theorem in Physics

The Ehrenfest Theorem in Physics

Introduction

• The Ehrenfest Theorem is one of the most important ideas in quantum physics. It shows how quantum systems change over time in a way that is similar to how regular systems change over time.
• This theory, which was first put forward by Paul and Tatiana Ehrenfest in 1927, has been very important in helping us understand how quantum systems work, especially during the quantum-classical transition.

Different Types of Mechanics: Classical and Quantum

Before you can understand the Ehrenfest Theorem, you need to know about classical mechanics and quantum mechanics, which are the two main ideas in current physics.

Classical Mechanics

• Describes the way objects move under the influence of forces.
• As long as you know where the particles are and how fast they are moving, you can use this framework to predict their behavior.

Quantum Mechanics

• Describes the behavior of particles in terms of their probabilities using wave functions.
• Unlike classical physics, quantum mechanics does not provide a definite way to describe how particles behave.
• Instead, it predicts the probability of finding a particle in a certain area of space.
• It also presents the idea of the Uncertainty Principle, which states that it is impossible to measure both position and momentum at the same time with absolute precision.

The Ehrenfest Theorem

• The Ehrenfest Theorem establishes a link between classical mechanics and quantum mechanics.
• It shows how the expected values of position and momentum change over time in quantum systems and how they relate to the fundamental equations of motion.

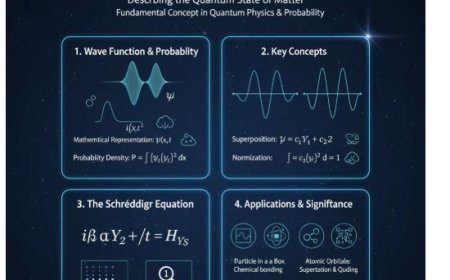
Mathematical Formulation

The Ehrenfest Theorem can be written mathematically as:

where:

Meaning of the Ehrenfest Theorem

• The theorem states that the way position and momentum change over time in a quantum system is similar to how they change in a classical system.
• This means:

• • The expectation values of position and momentum follow the same equations of motion as their classical counterparts.
  • The way these values evolve over time is similar to Newton's second law of motion.
  • However, this does not mean that individual quantum systems follow classical equations of motion.

Examples and Applications

There are many uses for the Ehrenfest Theorem in different areas of science. Below are three examples that show how important the Ehrenfest Theorem is.

Quantum Oscillator

• In quantum physics, the quantum oscillator is one of the most important systems.
• In the classical limit, the quantum oscillator behaves like a harmonic oscillator.
• The Ehrenfest Theorem plays a key role in understanding how this system transitions from quantum to classical behavior.

Quantum Spin

• Particles have a fundamental property called quantum spin, which describes their intrinsic angular momentum.
• The Ehrenfest Theorem helps analyze how the expectation values of spin components change over time, providing insight into the behavior of quantum spin systems.

Quantum Chaos

• Quantum chaos studies how quantum systems behave under chaotic conditions.
• The Ehrenfest Theorem helps us understand how quantum systems exhibit random behavior, highlighting similarities and differences between classical and quantum chaos.

Problems and Criticisms

Even though the Ehrenfest Theorem is important, it has some problems and limitations:

1. It cannot explain all quantum phenomena using classical equations of motion.
• The theorem applies only to expectation values, not to individual particle trajectories.
2. It does not provide a deterministic explanation of particle behavior.
• Quantum effects such as wave-particle duality and entanglement cannot be explained by the Ehrenfest Theorem.
3. It does not address the measurement problem in quantum mechanics.
• The theorem does not explain wave function collapse, which occurs when a measurement is made.