Fermi’s Golden Rule and Transitions Between Continuum States
Fermi’s Golden Rule explains how fast a quantum system transitions from one state to another under the influence of a small time-dependent disturbance. Derived from time-dependent perturbation theory, it calculates transition rates between discrete and continuum states using the system’s Hamiltonian and the density of final states. This rule is vital for understanding decay rates, scattering, and light-matter interactions such as the photoelectric effect and stimulated emission. It forms the foundation of modern quantum transition analysis in atomic, nuclear, and solid-state physics.
Fermi's Golden Rule and How It Helps Move Between Continuum States
- Fermi's Golden Rule is one of the most important ideas in quantum physics. It shows how quickly a quantum system changes from its first state to its final state.
- It's very important when working with continuum states, where the end states aren't separate energy levels but instead form a continuum.
Quantum Transitions and the Speed of Transitions
- The rate at which a quantum system changes from a starting state to a final state is called its transition rate.
- This rate is also called its transition chance per unit time.
- We need to know:
- The system's Hamiltonian
- Its starting and ending states
- Any other changes that might cause the transition to figure out the transition rate.
- First, there is time-dependent perturbation theory, which is a way to look at quantum systems that have small changes that happen over time.
- The system's Hamiltonian is split into two parts in this method:
- A part that doesn't depend on time (H₀)
- A part that does depend on time (H')
- Time-dependent perturbation theory is where Fermi's Golden Rule comes from.
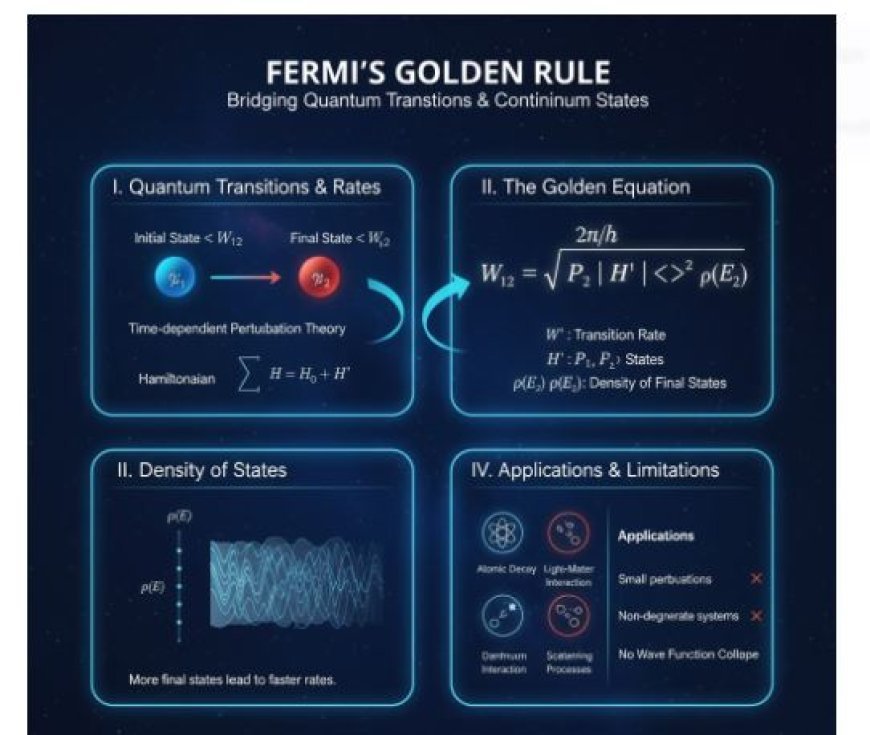
How to Get Fermi's Golden Rule
- To get Fermi's Golden Rule, you use time-dependent perturbation theory to figure out the transition amplitude between the starting and final states.
- Then, to get the transition rate, the absolute value of the transition amplitude is squared and all possible end states are integrated.
- The following statement is what this leads to:
Where:
- W₁₂ is the transition rate from state 1 to state 2.
- Ψ₁ and Ψ₂ are the initial and final wave functions.
- H' is the perturbation Hamiltonian.
- ρ(E₂) is the density of final states at energy E₂.
1. The Part of the Number of States
- A very important part of Fermi's Golden Rule is the density of states, ρ(E₂).
- It shows how many end states there are in a unit energy period.
- When working with continuum states, the number of states can be many times higher than the number of discrete states.
- This means that change rates are much faster.
2. Uses of Fermi's Golden Rule
Fermi's Golden Rule can be used for many things, such as:
- Figuring out how fast excited atomic and nuclear states decay.
- Describing interactions between electrons and photons, like photoelectric absorption and stimulated emission.
- Looking at scattering processes, like electron-electron or electron-phonon scattering.
3. Notations
- Fermi's Golden Rule has some restrictions, like assuming that changes are small and that it can only be used on non-degenerate systems.
- That being said, these problems can be fixed with:
- Additions and more complex methods.
- Time-independent perturbation theory.
- Density matrix approach.
What's Your Reaction?
arulprasanth
Arul Prasanth - MSc Geology graduate offering comprehensive study materials in Geology, Physics, and English. With a focus on clarity and effectiveness, I aim to provide students with the tools necessary for academic success.
