HISTOGRAM AND ITS APPLICATIONS
Histograms Reveal Rock & Sediment Grain Sizes at a Glance.
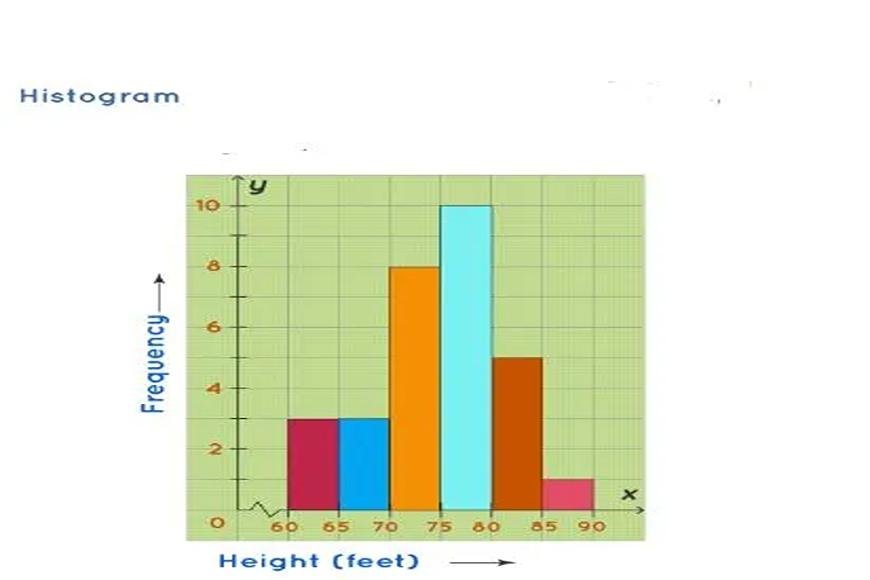
HISTOGRAM
- A histogram is a graph that shows a frequency distribution with continuous groups that are grouped.
- It's an area diagram, which means it's made up of rectangles whose bases are the gaps between class borders and whose areas are proportional to the rates in those classes.
- All the rectangles are next to each other in these kinds of pictures because the base fills the spaces between the class borders.
- For frequencies in the same class, the heights of shapes are related to each other, and for frequencies in different classes, the heights are related to the densities of those frequencies.
- To put it another way, a histogram is a graph with squares whose area is equal to the variable's frequency and its width is equal to the class interval.
Types of Histograms
- Based on how the frequencies are spread out in the data, the histogram can be put into different groups. One type of distribution is the normal distribution.
- Others are the skewed distribution, the bimodal distribution, the multimodal distribution, the comb distribution, the edge peak distribution, the heart cut distribution, the dog food distribution, and so on.
- You can use the histogram to show these different kinds of distributions.
There are four types of histograms:
Uniform Histogram
Symmetric histogram
Bimodal Histogram
Probability histogram
Uniform histogram
- As a regular distribution demonstrates, there shouldn't be so few classes.
- Each class has the same number of parts. It could have a distribution with more than one peak.
Bimodal Histogram
- It is called bimodal if a histogram has two points.
- When two different types of people or groups are observed in a data set and the centres of the two different histograms are far enough apart to show the variability in both sets, this is called bimodality.
Symmetric Histogram
- This type of histogram is also known as a bell-shaped histogram.
- If you draw a line down the middle of the histogram and the two sides are the same size and shape, we say that the histogram is symmetric.
- If the right half of the picture is the same as the left half, the diagram is exactly symmetric. Histograms that aren't straight are called "skewed."
Probability Histogram
- There is a picture of a discrete probability distribution called a probability histogram. It's made up of a rectangle centred on each value of x.
- The area of each rectangle is equal to the chance of that value happening. To start the probability histogram plot, the classes must be chosen.
- The heights of the bars in the graph show how likely each event is to happen.
Applications of Histograms
When we learn about different types of distributions, we can see how histograms can be used.
The normal distribution
- The structure that looks like a bell curve most of the time is called a normal distribution.
- In a normal distribution, the data points are just as likely to be on one side of the mean as they are on the other. It is important to keep in mind that some distributions look like normal distributions. There are formulas in statistics that can be used to show that a distribution is normal. It's important to remember that "normal" refers to a process's unique range.
- One example is that in some processes, there is a natural limit on one side that will cause skewed distributions. In the event that the distribution isn't thought to be normal, this is standard for the processes.
Skewed Distribution
- When there is a natural limit, the uneven distribution doesn't have the same end results on both sides.
- The distribution's top is off-centre in the direction of the limit, and its tail goes out a long way from it.
- For example, a spread of tests on a product that hasn't been tampered with would be skewed because the product can't be more than 100% pure.
- Natural limits also apply to holes that can't be smaller than the drill's width or call-receiving times that can't be less than zero.
- Depending on which way the tail points, the above distributions are called right-skewed or left-skewed.
Multimodal Distribution
- The plateau distribution is another name for the multimodal distribution.
- A bunch of different processes with normal distributions are put together.
- The end of the distribution looks like a plateau because there are many points close to each other.
Edge peak distribution
- The only difference between this distribution and the normal distribution is that this one has a bigger peak at one tail.
- All too often, it's because the histogram wasn't built correctly, with data grouped together into a collection called "greater than."
Comb Distribution
- In this pattern, there are bars that are both tall and short. Most of the time, it's because the data is cut off or the histogram was made wrong.
- This means that if the width of the histogram bar was 0.1o, the temperature that is rounded to the nearest 0.2o would show a shape that looks like a comb.
Truncated or heart-cut distribution
- With the tails cut off, the above distribution looks like a normal distribution.
- The maker may be making a normal range of products and then relying on inspection to tell them what is within the limits of the standard and what is not.
- The package that is sent to the end user based on the requirements is heart-cut.
Dog food distribution
- There is something missing from this release. The outcome is relatively comparable to the mean.
- Someone else is getting a heart-cut distribution, and the end-user who is left gets dog food, which is the meat scraps that are left over after the master has eaten.
- The item is put into two groups, one close to the upper specification limit and the other close to the lower specification limit.
- This is done so that the end user gets something that is within the limits of the specifications. This difference messes up the end user's process.
What's Your Reaction?