Neutrino Hypothesis, Fermi’s Theory of Beta Decay, and Selection Rules in Gamma Radiation

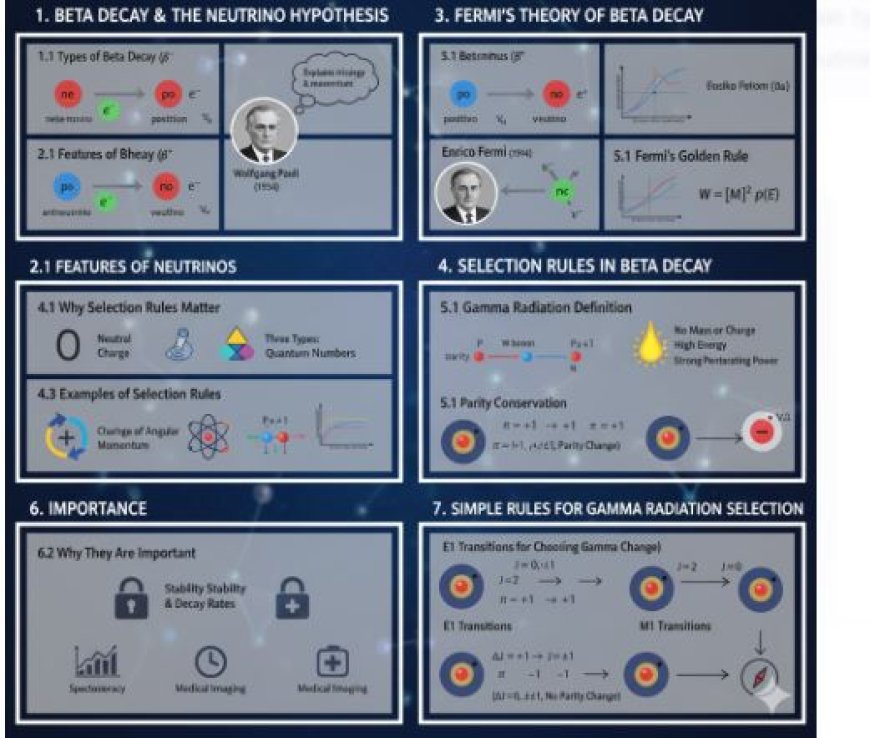
1.1 Types of Beta Decay

Beta decay occurs in two main types:

1. Beta-minus decay (β-): A neutron in an atom changes into a proton, releasing an electron (called a beta particle) and an antineutrino.
2. Beta-plus decay (β+): A proton in an atom changes into a neutron, releasing a positron (the opposite of an electron) and a neutrino.

2. The Neutrino Hypothesis

In 1930, Wolfgang Pauli proposed the existence of neutrinos—very light particles with no electric charge. Pauli suggested that neutrinos exist to explain the missing energy and momentum in beta decay.

2.1 Features of Neutrinos

• Neutral Charge: Neutrinos have no electric charge, allowing them to pass through matter unnoticed.
• Tiny Mass: Neutrinos have an extremely small mass, making them almost massless and capable of moving at high speeds.
• Three Types of Neutrinos:
• Electron neutrino (νₑ)
• Muon neutrino (νμ)
• Tau neutrino (ντ)

3. Fermi's Theory of Beta Decay

In 1934, Enrico Fermi developed a theory explaining beta decay, incorporating the newly proposed neutrinos. His theory describes how weak interactions occur during decay processes.

3.1 Important Ideas in Fermi's Theory

• Weak Interaction:
• Beta decay occurs due to the weak nuclear force, one of the four fundamental forces of nature.
• The W boson mediates this force, enabling the conversion of neutrons into protons.
• Fermi's Golden Rule:
• This principle calculates the probability of a system transitioning between different quantum states.
• It helps estimate the rate of beta decay.

4. Rules for Choosing in Physics

Selection rules are crucial in quantum physics as they determine which transitions between energy states are allowed in atomic and subatomic systems.

4.1 Why Selection Rules Matter

• Simplifies Complex Systems: Helps in understanding quantum systems by defining which transitions are possible.
• Quantum Numbers: Transitions depend on properties such as angular momentum and parity, described by quantum numbers.

4.2 How It Relates to Beta Decay

In beta decay, selection rules determine which particle transitions occur during emission. These rules apply to changes in rotational momentum and parity.

4.3 Examples of Selection Rules

• Change in Angular Momentum (ΔL): The change in orbital angular momentum must be ±1.
• Conservation of Parity: The overall parity of the initial and final states must remain consistent.

5. Rules for Selecting Gamma Radiation

Gamma radiation is a fundamental concept in nuclear physics, particularly in the study of radioactive decay and interactions with matter.

5.1 Gamma Radiation Definition

Gamma radiation is high-energy electromagnetic radiation emitted by an atom's nucleus during nuclear decay or reactions. Unlike alpha and beta radiation, gamma rays:

• Have no mass or charge.
• Possess extremely high energy.
• Have strong penetrating power, allowing them to pass through materials more effectively than alpha and beta particles.

6. Importance of Selection Rules in Gamma Radiation

6.1 Guidelines for Choosing

Selection rules are theoretical principles that predict the likelihood of specific transitions in quantum systems. They help determine which nuclear transitions allow the emission or absorption of gamma radiation.

6.2 Why They Are Important

Selection rules help:

• Predict the probability of gamma emission.
• Understand nuclear energy levels and angular momentum.
• Interpret spectroscopic data.

7. Simple Rules for Choosing Gamma Radiation

7.1 Change in Angular Momentum (ΔJ)

• Allowed Transitions:
• Gamma emissions typically occur when total angular momentum (J) changes by ±1 or 0.
• Example: J = 2 → J = 1 or J = 0 → J = 1.
• Forbidden Transitions:
• Transitions where ΔJ > 1 (e.g., J = 2 → J = 0) are less likely.

7.2 Parity Conservation

• Definition: Parity refers to the wavefunction symmetry under spatial inversion.
• Rules:
• If the initial state has positive parity (π = +1), the final state must also have positive parity.
• If the initial state has negative parity (π = -1), the final state must also have negative parity.

7.3 Change in Magnetic Quantum Number (ΔM)

• Definition: This quantum number represents the orientation of angular momentum.
• Allowed Transitions:
• The change in the magnetic quantum number (ΔM) must follow:
• ΔM = 0 or ±1 → These transitions are the most common.

7.4 Electric and Magnetic Dipole Transitions

Gamma transitions can be classified based on their interaction type:

• Electric Dipole (E1) Transitions:
• The most common type.
• Follow ΔJ = ±1 and require a parity change.
• Highly probable.
• Magnetic Dipole (M1) Transitions:
• Allow ΔJ = 0 or ±1, but parity remains unchanged.
• Less likely compared to E1 transitions.
• Higher Multipole Transitions (E2, E3, M2, etc.):
• More complex and occur less frequently.

8. Effects of Selection Rules

8.1 Spectroscopy

Selection rules help scientists analyze nuclear energy levels and determine the structure of atomic nuclei using spectroscopy.

8.2 Stability and Decay Rates

• The stability of isotopes depends on allowed transitions.
• Unstable isotopes with many possible transitions decay faster.

8.3 Practical Applications

Selection rules for gamma radiation have applications in various fields:

• Medical Imaging: Used in PET scans and radiation therapy.
• Nuclear Energy: Helps understand radioactive decay in nuclear reactors.
• Astrophysics: Used in gamma-ray astronomy to study cosmic events.